Haskell part 2, much better solution

Okay, here’s the outline again - this one ran instantly.

Rather than probing with example values, I took a different approach, debugging the structure. I only really care about inputs and outputs, so I wrote something that turns the “wiring diagram” into a map of label -> Expr, where

data Expr = EInput String
          | EAnd Expr Expr
          | EOr Expr Expr
          | EXor Expr Expr
  deriving (Show, Ord)

(the Eq instance is stable in symmatric expressions, eg (==) (EAnd a b) (Eand c d) = a == c && b == d || a == d && b == c)

The expressions are grounded in “inputs” (“x00”…“x44”, “y00”…“y44”) - that is, they just expand out all of the intermediary labelled things.

Then I constructed a circuit that I was after by building a non-swapped 44/45-bit full adder, and produced the same set of expressions for those.

Then: for each output, z00…z45, check the “spec” expression against the actual one. If they’re identical, move on.

Otherwise, find some candidate pairs to swap. For these, I considered all possible labelled outputs except “stable” ones - that is, those that were input depdendencies of z_(i-1) - ie, don’t swap any outputs involved in the computation that’s validated thus far.

searchForSwap :: Exprs -> Layout -> String -> Set.Set String -> [(String, String, Layout, Exprs)]
searchForSwap eSpec actual zz stable =
  let
    vals = Map.keysSet actual & (`Set.difference` stable) & Set.toList
    ds = dependencies actual
  in do
    k1 <- vals
    k2 <- vals
    guard $ k1 < k2
    guard $ k1 `Set.notMember` (ds Map.! k2)    -- don't create any loops
    guard $ k2 `Set.notMember` (ds Map.! k1)
    let actual' = swapPair k1 k2 actual
        eAct' = exprsForLayout actual'
    guard $ eSpec Map.! zz == eAct' Map.! zz
    pure (k1, k2, actual', eAct')

Taking the new layout with swapped outputs and its corresponding set of expressions, carry on searching as before.

A linear scan over the output bits was all that was required - a unique answer poped out without any backtracking.

Anyway, happy Christmas all.

PS. My other version worked (eventually) - it was following this approach that led me to realise that my “spec” full adder was broken too :-D Never skip the unit tests.

(@CameronDev@programming.dev you were asking about alternatives to graphviz-style approaches I recall)

Haskell, programmatic solution

I spent an entire day on this because I didn’t write a unit test to check my “swap outputs” function, which effectively did nothing.

In any case: the approach (which may be more interesting than the code, I know people were interested) involved probing the addition circuit with some example additions - that is, I wrote something that’d let me give alternative inputs from x & y and compute the result using the circuit. I then gave it some simple pairs of values that’d exercise the add and carry bits (ie, pairs chosen from {i << n, n <- {1..43}, i <- {1, 3}}). That gave me some breaking trials.

Because the errors were relatively sparse, I then scanned over pairs of outputs, swapping those that didn’t introduce a data dependency and checking (a) that no new errors were introduced over the trial sets, (b) for any reduction in the number of errors found. I got a bunch fo outputs like this:

swap of ("ccp","mnh") improves matters
bad trial count reduced from 346 to 344

which found the pairs for me. The search could be improved by more carefully tying the probe inputs to the outputs’ dependencies (ie, if the first error comes from the (xi, yi) input bits, then look for swaps of the dependencies introduced by zi) - but in any case, it finds the answer. Phew.

Rust + Pen and Paper

Yikers. Part 2 took a while, staring at this diagram for hours. Eventually I noticed that each of these blocks has two pairs of (XOR, AND) gates sharing the same inputs (and inputs aren’t changed). So I matched up these pairs based on a distance metric of how much needs to be swapped to fit together. This helped me identify 4 blocks with errors, the rest was solved using pen and paper (one block is missing as it became apparent at that point):

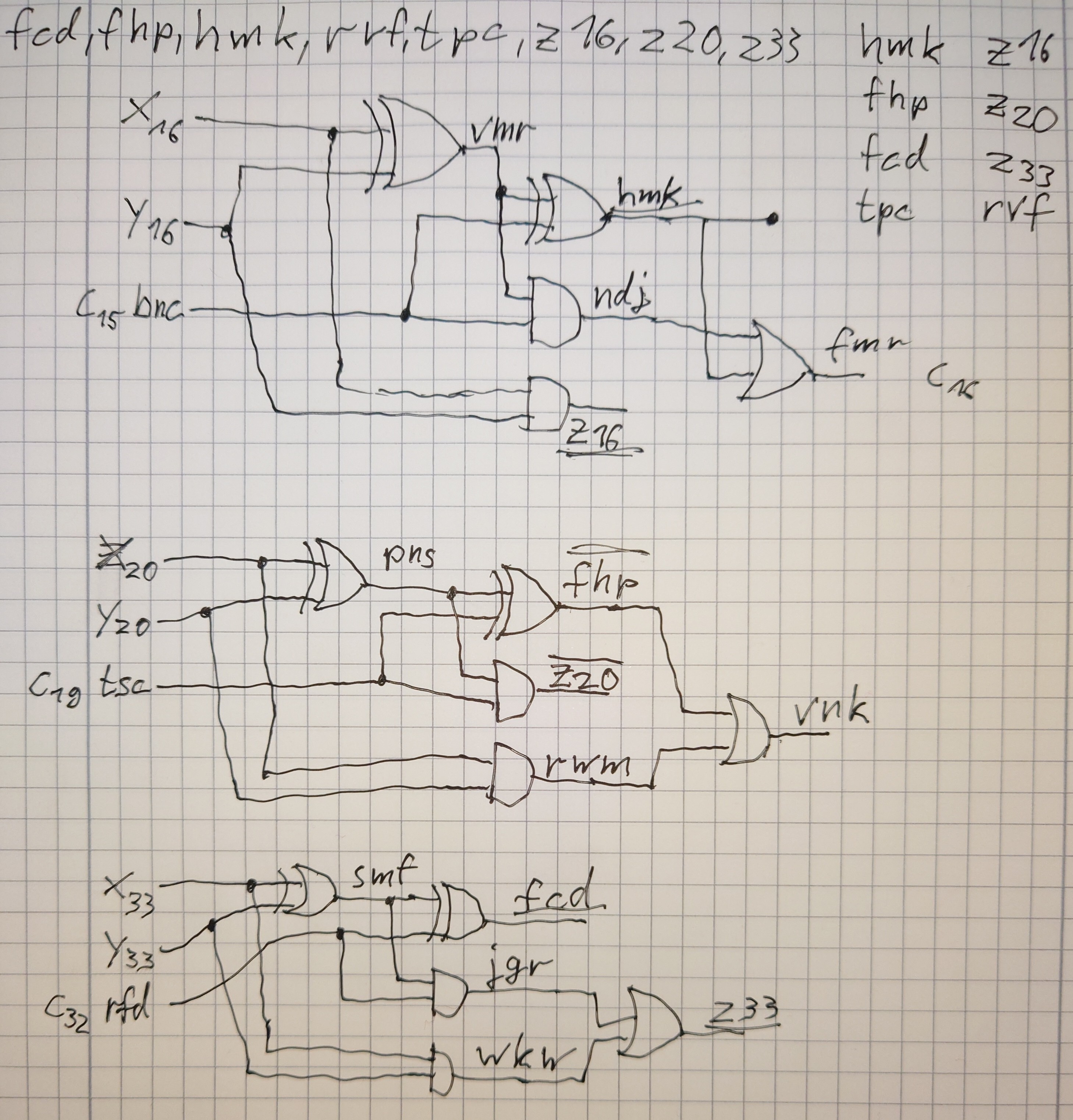
There is also some code, but do yourself and me a favor and don’t look at it. While it does turn up the correct solution, it probably won’t with any other input, especially not the examples.